Белорусский государственный медицинский университет
2.Костная перегородка носа
, septum nasi osseum. Образована, главным образом, сошником и перпендикулярной пластинкой решетчатой кости. Рис. В. См. 136.4. 3.Грушевидная апертура, (передняя носовая)
, apertura piriformis (nasalis anterior). Отверстие, ведущее в носовую полость. Рис. А, Рис. В, Рис. Г. 4.Верхний носовой ход
, meatus nasalis superior. Расположен выше средней носовой раковины. Рис. А. 5.Средний носовой ход
, meatus nasalis medius. Расположен между средней и нижней носовыми раковинами. Рис. А. 6.Нижний носовой ход
, meatus nasalis inferior. Расположен под нижней носовой раковиной. Рис. А. 7.Носослезный канал
, canalis nasolacrimalis. Содержит носослезный проток, который открывается под нижней носовой раковиной. Рис. В. 8.Клиновидно-решетчатое углубление
, recessus sphenoethmoidalis.
Пространство, расположенное выше верхней носовой раковины. Рис. А. 9.Носоглоточный ход
, meatus nasopharyngeusХоаны
, choanae. Отверстия, ведущие из полости носа в носоглотку. Рис. А. 11.Клиновидно-небное отверстие
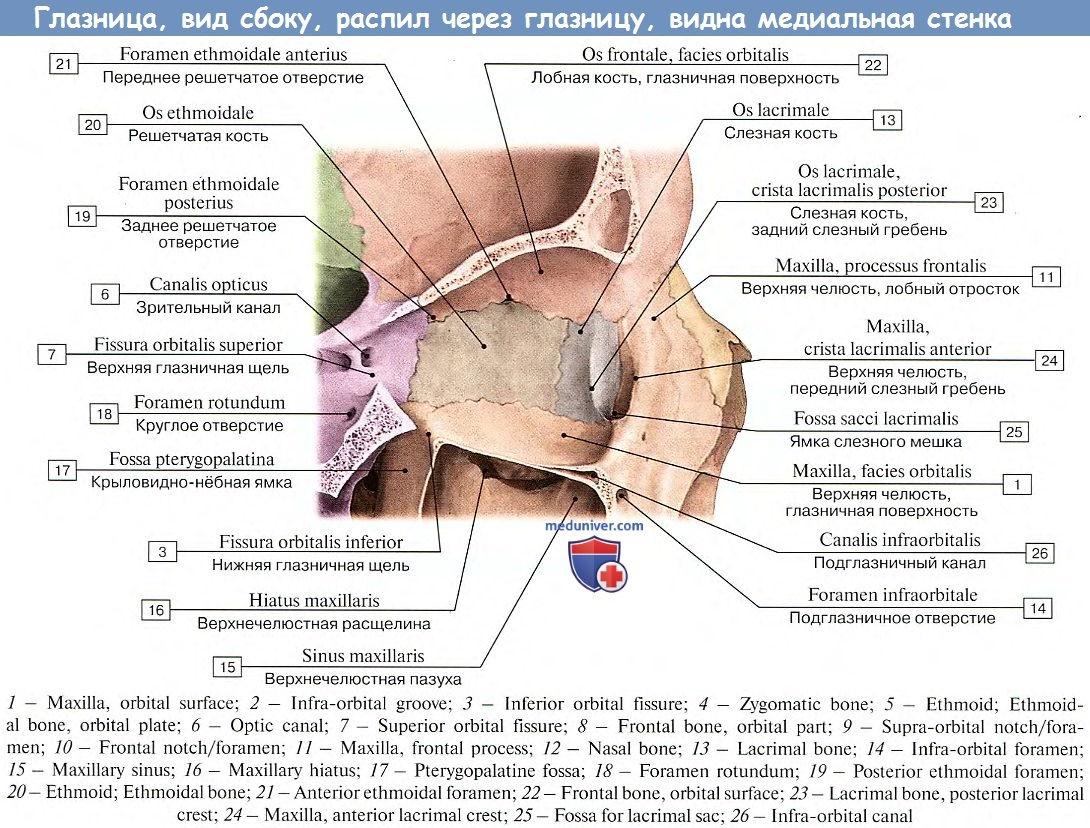
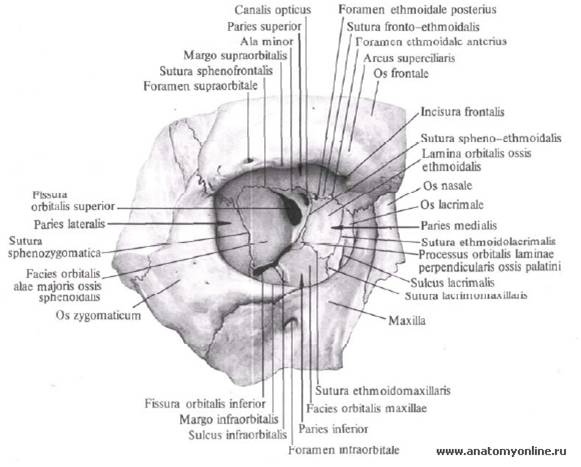
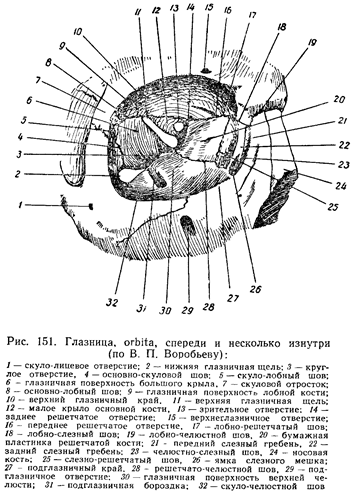
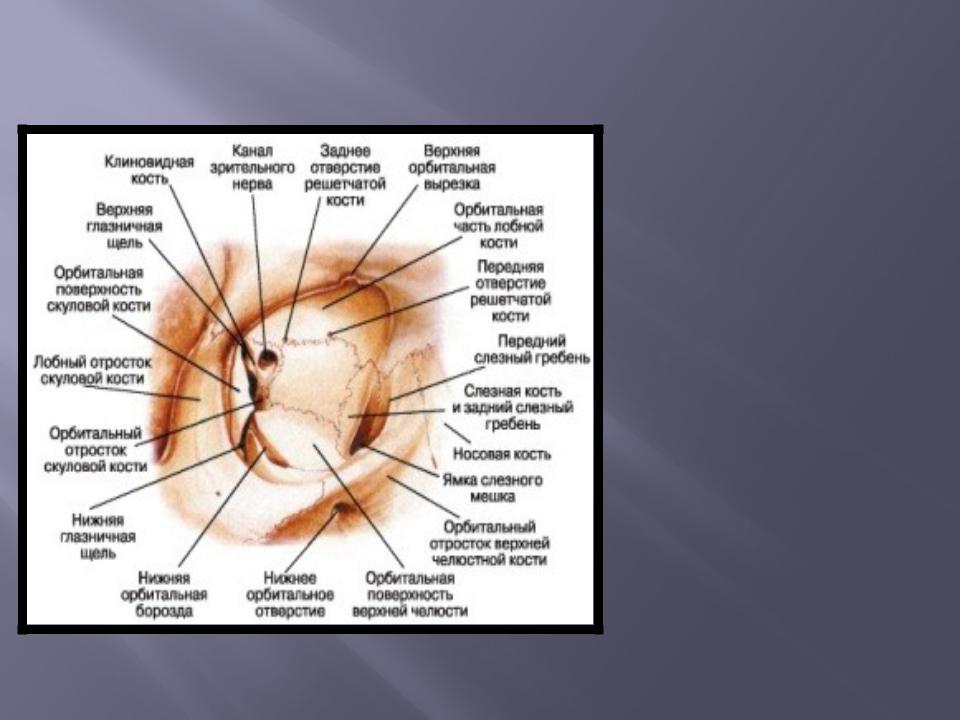
, foramen sphenopalatinum. Образовано одноименной вырезкой небной и телом клиновидной костей. Соединяет между собой верхнюю часть крыловидно-небной ямки и носовую полость. Рис. А. 12.Глазница
, orbita. Костная полость, которая содержит глазное яблоко. Рис. В, Рис. Г. 13.Вход в глазницу
, aditus orbitalis. Переднее отверстие (основание) глазницы. Рис. Г.14.
Глазничный край
, margo orbitalis. 15.Надглазничный край
, margo supraorbitalis. Верхний край входа в глазницу. Рис. В. 16.Подглазничный край
,
Нижний край входа в глазницу. Рис. В.16a.
Латеральный край
, margo lateralis.16б.
Медиальный край
, margo medialis. 17.Верхняя стенка
, paries superior. Крыша глазницы. Рис. В. 18.Нижняя стенка
, paries inferior. Дно глазницы. Рис. В. 19.Латеральная стенка
, paries lateralis. Рис. В. 20.Медиальная стенка
, paries medialis. Рис. В. 21.Переднeе решетчатое отверстие
, foramen ethmoidale anterius. Расположено на медиальной стенке глазницы между лобной и решетчатой костями. Через него проходят передние решетчатые нерв и сосуды. Рис. В. 22.Заднее решетчатое отверстие
,Слезная борозда
, sulcus lacrimalis. Находится у начала носослезного канала.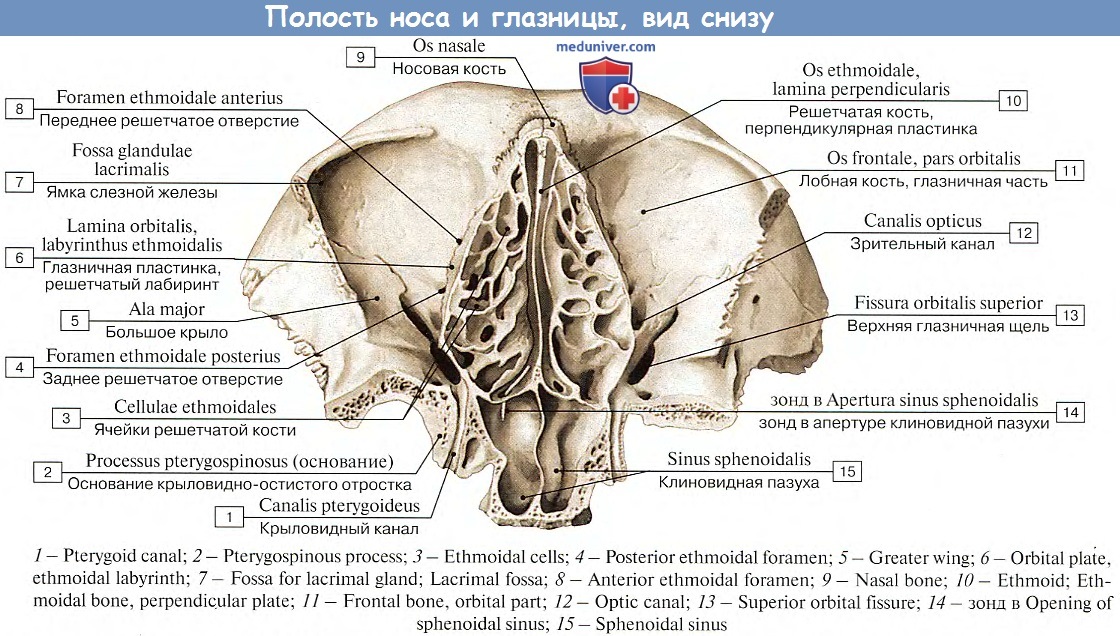
Рис. В. См. 20. 23 23.Верхняя глазничная щель
, fissura orbitalis superior. Расположена в задней части боковой стенки глазницы между большими и малыми крыльями клиновидной кости. Соединяет полость черепа с глазницей и содержит глазной, глазодвигательный, блоковый и отводящий нервы, а также v.ophthalmica superior. Рис. В. 24.Нижняя глазничная щель
,ЗАТЫЛОЧНАЯ НОРМА
, norma occipitalis. Вид черепа сзади. Рис. Б.25a.
Инион
, inion. Соответствует центру наружного затылочного выступа. 26.Ламбда
, lambda. Место соединения ламбдовидного и сагиттального швов черепа. Рис. Б. 27.Роднички черепа
, fonticuli cranii. Неокостеневшие соединительнотканные промежутки между костями cвода черепа у плодов и детей.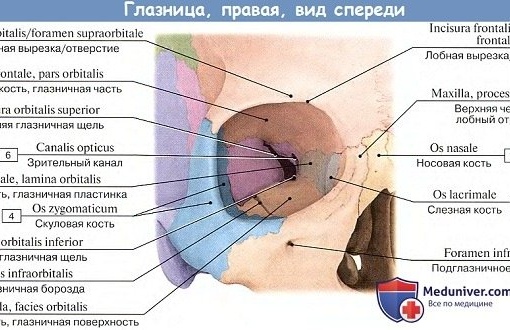
Передний родничок
, fonticulus anterior. Имеет ромбовидную форму и расположен между двумя половинами лобной и теменными костями. Зарастает на втором году жизни. Рис. Г, Рис. Д. 29.Задний родничок
, fonticulus posterior. Находится между теменными и затылочной костями. Зарастает у детей на третьем месяце жизни. Рис. Г, Рис. Д. 30.Клиновидный (переднелатеральный) родничок
, fonticulus sphenoidalis (anterolateralis). Расположен на боковой поверхности черепа между лобной, теменной, височной и клиновидной костями. Соответствует птериону. Рис. Г. 31.Сосцевидный родничок (заднелатеральный)
, fonticulus mastoideus (posterolateralis). Находится между теменной, затылочной и височной костями. Соответствует астериону. Рис. Г.Белорусский государственный медицинский университет
1.РЕШЕТЧАТАЯ КОСТЬ
,
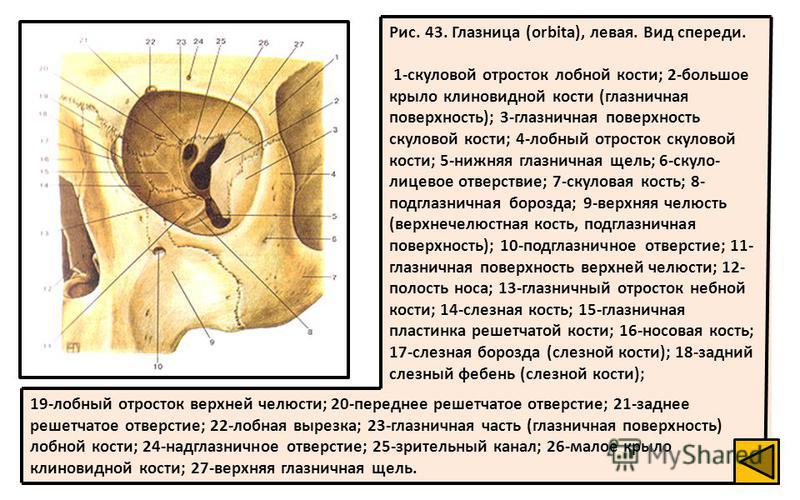Рис. А, Рис. Б, Рис. В, Рис. Г. 2.Решетчатые пластинка и отверстия
, lamina et foramina cribrosa. Пластинка расположена горизонтально и отделяет носовую полость от передней черепной ямки. Решетчатые отверстия содержат обонятельные нервы. Рис. Б. 3.Петушиный гребень
, crista galli. Направлен в полость черепа. Место прикрепления серпа мозга. Рис. А, Рис. Б, Рис. В, Рис. Г. 4.Крыло петушиного гребня
, ala cristae galli. Парные отростки, при помощи которых crista galli прикрепляется к лобному гребню. Рис. А, Рис. Б, Рис. В, Рис. Г. 5.Перпендикулярная пластинка
,6.
Решетчатый лабиринт
, labyrinthus ethmoidalis. Воздухоносные ячейки, расположенные между глазницей и полостью носа. 8.Решетчатая воронка
, infundibulum ethmoidale. Узкий ход между крючковидным отростком и большим решетчатым пузырьком под средней носовой раковиной.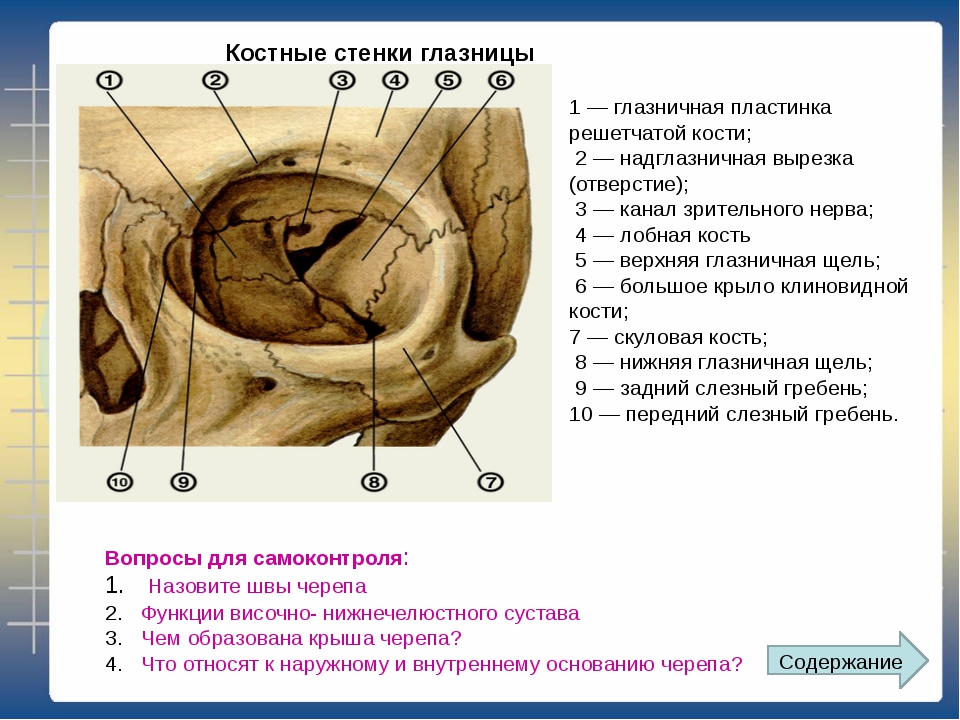
В него открываются лобная и верхнечелюстная пазухи, передние ячейки решетчатой кости. Рис. А, Рис. В. 9.Полулунная расщелина
, hiatus semilunaris. Отверстие, через которое решетчатая воронка сообщается с носовой полостью. Рис. В. 10.Большой решетчатый пузырек
,Глазничная пластинка [[бумажная]]
, lamina orbitalis [[lamina papyracea]]. Oчень тонкая костная пластинка, формирующая часть медиальной стенки глазницы . Рис. В. 12.Решетчатые отверстия
, foramina ethmoidalia. Расположены по краю кости, которым она соединяется с os frontale. Содержит решетчатые сосуды и нервы. Рис. В. 13. [Наивысшая носовая раковина
, concha nasalis suprema]. Тонкая костная пластинка. Присутствует непостоянно. Рис. Г. 14.Верхняя носовая раковина
, concha nasalis superior.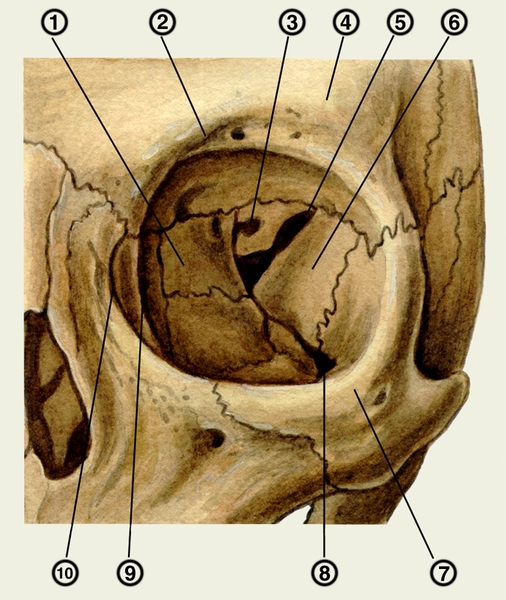
Крючковидный отросток
, processus uncinatus. Направлен назад и вниз. Почти полностью прикрыт средней носовой раковиной и частично закрывает полулунную расщелину. Рис. А, Рис. В. 17.НИЖНЯЯ НОСОВАЯ РАКОВИНА
, concha nasalis inferior. Самостоятельная кость на латеральной стенке носовой полости. Рис. Д.18.
Слезный отросто
Белорусский государственный медицинский университет
3.Наружная поверхность
, facies externa. Рис. А. 4.Лобный бугор (лобное возвышение)
, tuber frontale (eminentia frontalis). Рис. А. 5.Надбровная дуга
, arcus superciliaris. Возвышение выше надглазничного края. Рис. А, Рис. Б. 6.Глабелла
,6a. [
Лобный шов
, sutura frontalis]. У плодов и детей раннего возраста разделяет лобную чешую на две половины. 8.Надглазничная вырезка / отверстие
, incisura supraorbitalis / foramen supraorbitale.
Расположено на надглазничном крае. Место выхода надглазничной артерии и латеральной ветви надглазничного нерва. Точка пальцевого прижатия первой ветви тройничного нерва. Рис. А, Рис. Б. 9.Лобная вырезка (отверстие)
, incisura frontalis (foramen frontale). Расположена медиально от надглазничного отверстия. В ней проходят надблоковая артерия и медиальная ветвь надглазничного нерва. Рис. А, Рис. Б. 10.Височная поверхность
,Теменной край
, margo parietalis. Обращен назад и соединяется с теменной костью. Рис. А, Рис. В. 12.Височная линия
, linea temporalis. Продолжение височных линий теменной кости. Рис. А. 13.Скуловой отросток
, processus zygomaticus. Расположен латерально от глазницы и соединяется со скуловой костью. Рис. А, Рис. Б, Рис. В. 14.Внутренняя поверхность
, facies interna. Обращена к мозгу. Рис. В.
15.Лобный гребень
, crista frontalis. Костный выступ по середине внутренней поверхности лобной кости. Место прикрепления серпа мозга. Рис. В. 16.Борозда верхнего сагиттального синуса
,Слепое отверстие
, foramen caecum. Углубление кзади от лобного гребня, на дне которого иногда имеется отверстие для эмиссарной вены. Рис. В. 17a.Лобный (метопический) шов
, sutura frontalis (metopica). Сохранившийся у взрослых лобный шов. Рис. А. 18.Носовая часть
, pars nasalis. Расположена между двумя глазничными частями. Рис. А, Рис. Б. 19.Носовая ость
, spina nasalis. Расположена по средней линии носовой части. Рис. А, Рис. Б, Рис. В. 20.Носовой край
, margo nasalis. Зубчатый нижний край носовой части. Соединяется с носовыми костями. Рис. А, Рис. Б, Рис. В. 21.Глазничная часть
,
Формирует верхнюю стенку глазницы. Рис. А, Рис. Б, Рис. В. 22.Глазничная поверхность
, facies orbitalis. Обращена в сторону глазницы. Рис. Б. 23. [Блоковая ость
, spina trochlearis]. Небольшое возвышение в верхнемедиальном углу глазницы, к которому фиксируется блок верхней косой мышцы. Встречается непостоянно. Рис. А. 24.Блоковая ямка
, fovea trochlearis. Небольшое углубление для прикрепления хрящевого блока, через который перебрасывается сухожилие m.obliquus superior. Рис. А, Рис. Б. 25.Решетчатые отверстия
, foramina ethmoidalia. Cодержат одноименные сосуды и нервы. Рис. Б. 26.Ямка слезной железы
, fossa glandulae lacrimalis. Углубление, расположенное в латеральном углу глазницы. Содержит слезную железу. Рис. Б. 27.Решетчатая вырезка
, incisura ethmoidalis. Расположена между глазничными частями. Заполнена решетчатой костью. Рис. Б. 28.Лобная пазуха
, sinus frontalis.
Прилежит к верхней стенке глазницы. Её средние параметры: высота — 3 , ширина — 2,5 , передне-задний размер — 1,8 см. Сообщается через решетчатую воронку со средним носовым ходом. Рис. А. 29.Апертура лобной пазухи
, apertura sinus frontalis. Расположена на нижней стенке пазухи, ближе к средней линии. Рис. Б, Рис. В. 30.Перегородка лобных пазух
, septum intersinuale frontale. Cтенка между правой и левой пазухами. Рис. А.Решетчатая кость (os ethmoidale). Биомеханика, техники тестирования и коррекции
Анатомия решетчатой кости
Решетчатая кость (os ethmoidalis) – непарная кость мозгового отдела черепа, отделяет носовую полость от полости черепа располагается по средней линии.
Расположена срединно, между лобной костью (сверху), верхней челюстью (снизу) и клиновидной костью (сзади).
Строение
Состоит из четырех частей:
- вертикальная пластинка,
- горизонтальная пластинка,
- две латеральные массы, подвешенные к горизонтальной пластинке.
Горизонтальная пластинка (lamina cribrosa).
Плоская, имеет квадратную форму и множество (до 20) мелких отверстий, через которые проходят в полость черепа волокна обонятельного нерва. Посередине разделена выступающим вверх петушиным гребнем (crista galli) вертикальной пластинки, к которому крепится твёрдая мозговая оболочка. В передней части имеет переднее решётчатое отверстие, в котором проходят одноименная артерия и внутренний носовой нерв (V1). Также имеется два решётчатых желоба для обонятельных луковиц.
Вертикальная пластинка (lamina perpendicularis).
Тонкая, расположена в сагиттальной плоскости. Верхняя часть представляет собой петушиный гребень, к которому в его верхне-передней части крепится серп мозга. Передняя его часть заканчивается крыловидным отростком (processus alaris), сочленяющимся со слепым отверстием (foramen caecum). Нижняя часть вертикальной пластинки образует передне-верхнюю (костную) часть носовой перегородки.
Латеральные массы (решётчатый лабиринт, labyrinthus ethmoidalis).
Парное объёмное образование, относится к придаточным пазухам носа. «Подвешены» к латеральным краям горизонтальной пластинки, состоят из воздухоносных ячеек, которые сообщаются между собой и с полостью носа. Внешняя поверхность участвует в образовании стенки глазницы глазничной (бумажной) пластинкой (lamina orbitalis). Медиальная поверхность обращена в полость носа и несет на себе носовые раковины: среднюю (concha nasalis media), верхнюю (superior) и (вариант) наивысшую (suprema). Между верхней и средней носовой раковиной находится верхний носовой ход (meatus nasi superior), ниже средней раковины под её краем находится средний носовой ход (meatus nasi medius), снизу он ограничен верхним краем нижней носовой раковины. На заднем конце средней носовой раковины имеется изогнутый крючковидный отросток (processus uncinatus) для соединения с решетчатым отростком нижней носовой раковины. Сзади от него имеется выпячивание —- большой решетчатый пузырек (bulla ethmoidalis), представляющее собой одну из самых крупных ячеек лабиринта.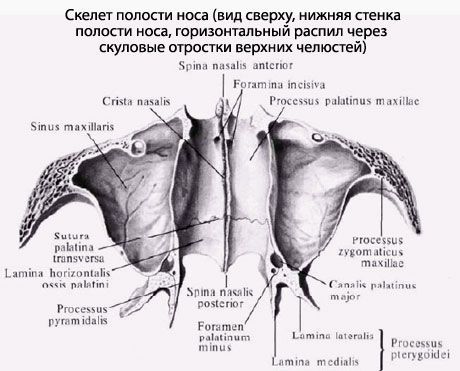
Между крючковидным отростком и решетчатым пузырьком имеется воронкообразная щель (решетчатая воронка, infundibulum ethmoidale), через которую средний носовой ход сообщается с лобной пазухой (sinus frontalis).
https://ru.wikipedia.org/wiki/Решётчатая_кость
Соединения решетчатой кости
1. С лобной костью (лобно-решетчатый шов, sutura frontoethmoidalis)
Верхняя поверхность латеральных масс и решетчатая пластинка решетчатой кости соединяются с полуячейками решетчатой вырезки лобной кости (гармоничный шов)
2. С клиновидной костью (клиновидно-решетчатый шов, sutura sphenoethmoidalis)
Задний край решетчатой пластинки решетчатой кости соединяется с этмоидальным шипом клиновидной кости. Гармоничный шов
Задний край перпендикулярной пластинки решетчатой кости соединяется с гребнем клиновидной кости. Гармоничный шов
Задние края латеральных масс решетчатой кости соединяются с передненаружными краями клиновидной кости. Гармоничный шов.
3. С небной костью (нёбно-решетчатый шов, sutura palatoethmoidalis)
Нижний край латеральных масс решетчатой кости соединяется с н
отверстие—отверстие | |
Заднее альвеолярное отверстие | |
заднее крестцовое отверстие | |
Заднее | |
Отверстие | |
Отверстие | |
Отверстие | |
решетчатое | cancellos |
заднее решетчатое отверстие | |
отверстие | |
отверстие | |
отверстие | |
отверстие | |
заднее сиденье | |
Заднее носовое отверстие | |
отверстие | |
отверстие | transfigo |
решетчатое | cancellos |
Заднее носовое отверстие | |
заднее решетчатое отверстие | |
заднее крестцовое отверстие | |
Заднее альвеолярное отверстие | |
отверстие | |
Отверстие | |
отверстие | |
отверстие | |
отверстие | |
Отверстие | |
отверстие—отверстие | |
Отверстие | |
Заднее | |
отверстие | transfigo |
заднее сиденье | |
отверстие |
Озвученные примеры.| Стяжки из бальзовой решетки приданы куполообразной форме верха. | |
| Модель с регулируемой горловиной, вид изнутри. Внутренняя облицовка — австралийская ярра. | |
| Регулируемый гриф с внутренним шестигранником между 17 и 18 ладами. При использовании грифа такого типа качество звука не ухудшается. | |
«Внутренности» регулируемой шеи. Он держится за струны. Есть небольшой паз и шип, который действует как вертикальный упор, а гриф поворачивается от горизонтального куска углеродного волокна.Установочный винт на грифе / грифе регулирует действие. | |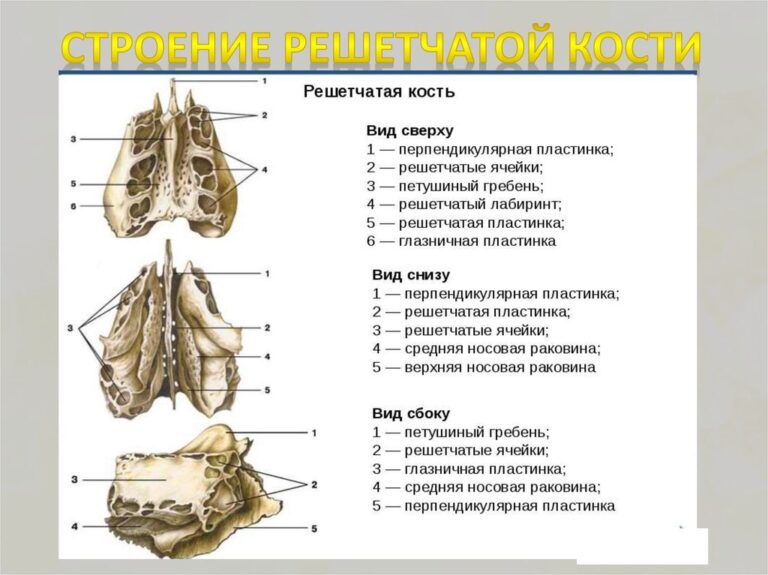
| Гитара натягивается до связывания и зачистки краев гитары, чтобы я мог окончательно настроить резонанс верха гитары. На этой фотографии представлен режим вибрации монополя. Вот Звуковой образец (1 МБ) модели регулируемого грифа до нанесения отделки. | |
| Модель с регулируемым вырезом имеет форму, отличную от формы пятки, что помогает предотвратить люфт в области шеи. | |
| Вот типичная последовательность облицовки боковых сторон. | |
| Свежий из формы. вид изнутри по бокам. | |
Свежий из формы.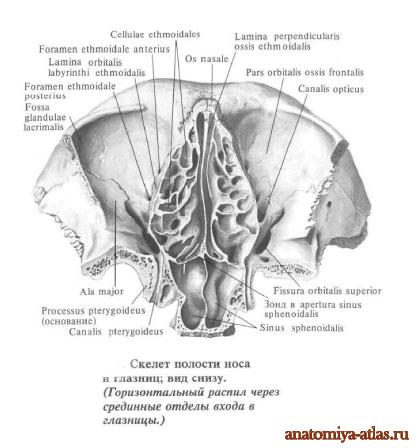 Внешний вид по сторонам. | |
| Внутри корпуса до прикрепления верха. | |
| Верхний упор цельный. Активен только нижний бой. Это не проблема, потому что верхняя часть не добавляет ничего существенного к звучанию гитары. | |
| Регулируемый гриф усилен стержнями из углеродного волокна и твердым кленом. | |
| Первые две гитары с решетчатой решеткой Schramm! Обратите внимание на подлокотник на этих гитарах. Подлокотник не позволяет игроку касаться верхней части, позволяя большей части вибрировать. | |
Вид сбоку. | |
| Спинка. | |
| Спинка модели регулируемой шеи. | |
| Модель верха с регулируемым вырезом. | |
| Молд для спины. | |
| Регулируемая шейная часть тела перед прикреплением спинки. | |
Лето 2008 г. Шасси с более глубокой задней частью. | |
| Шасси Summer 2008, вид сверху. | |
| Зачерпание распорки «А». | |
| Шасси Summer 2008, вид изнутри. | |
| 2008 дизайн. | |
| Модель 2008 года с усиленной бальзовой распоркой и углеродным волокном. | |
| Гитара с короткой решеткой, 630 мм. | |
Модель решетчатой гитары с приподнятым грифом 2008 года выпуска. | |
| Обратное формование в вакуумном прессе. | |
| Задняя часть снята с вакуумного пресса.Вид сзади изнутри. | |
| Задняя часть снята с вакуумного пресса. Внешний вид спины. | |
| Спинка вырезается. | |
| Прогиб спинки. Для этих спинок подтяжки не нужны. | |
| Готово к очистке. | |
2008 литая спинка. | |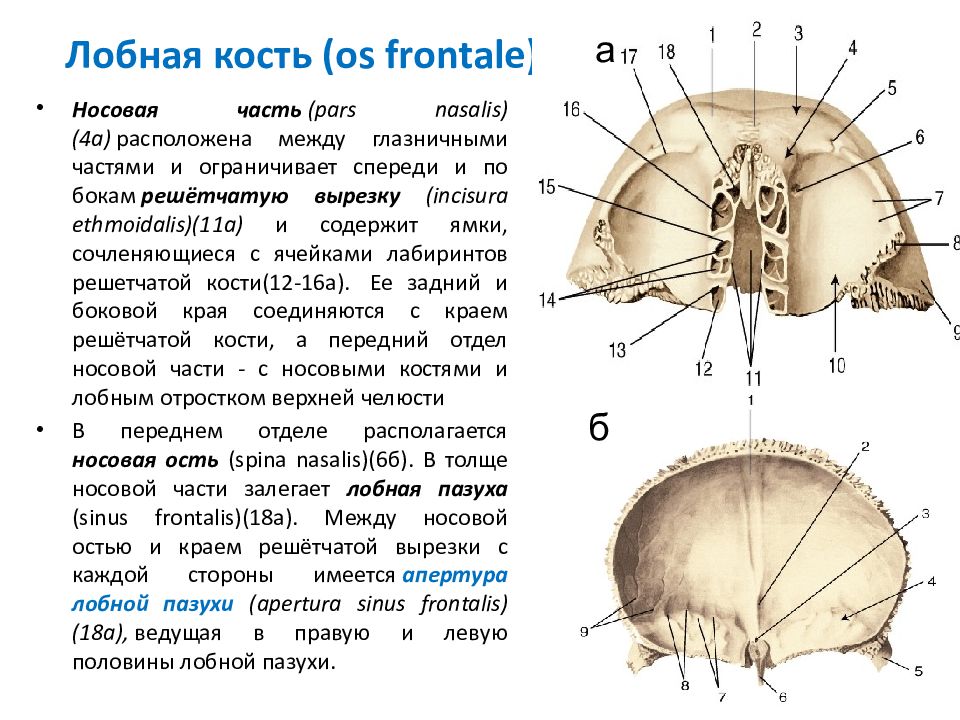
| Решетчатая гитара Schramm 2009 года выпуска с решеткой, приклеенной к деке с помощью вакуумного зажима. | |
| Построенная в августе 2008 года, эта решетчатая гитара имеет регулируемую систему грифа, аналогичную конструкции Грега Смоллмана. На этом этапе я «озвучиваю» инструмент с выключенной спинкой! Я удаляю древесину в определенных местах, чтобы настроить древесину и ощущение инструмента. Поверьте, не гитара звучит так же громко без спинки. Вот образец звука этой гитары без спинки до каких-либо настроек. Вот образец звука той же гитары после настроек. | |
| Крупный план той же гитары 2008 года выпуска. | |
2 типа решеток
2.
2
Решетки Bravais Там — неограниченное количество возможных решеток, поскольку нет ограничений на размер и угол между векторами решетки a , b и c . Решетки могут, однако их можно разбить на группы, инвариантные относительно определенных комбинации операций вращательной симметрии, указанные выше и ниже зеркальное отражение. Всего 5 таких типы решеток в 2-х измерениях и 14 типов в 3-х измерениях. Эти различные типы решеток называются решетками Браве после Огюст Браве, который в 1848 году показал, что существует 14 типов.
Рисунок 5: 14 решеток Браве; обратите внимание, что сферы представляют собой точки решетки
2,3 Закрыть упаковочные конструкции
Самый эффективный метод упаковка сфер в гексагональных слоях. 3 сферы в таком слое образуют долину, в которой сфера из слоя выше сидит.
Рисунок 6: Слой плотно упакованных сфер
Первый слой сфер — это
помечены A, второй B.
третий слой может быть добавлен непосредственно поверх первого слоя (другой слой A) или
в альтернативной позиции C. Оба
устройства дают структуры плотной упаковки.
Расположение ABABAB обозначено шестиугольником.
плотно упакованный (ГПУ) и расположение ABCABC помечено как грань
центрированный кубический (ГЦК) или кубический
плотно упакованный (ccp) .
Поскольку атомы и ионы в кристаллические структуры обычно моделируются как твердые сферы (и это обычно разумное приближение), эти договоренности часто наблюдаются потому что они увеличивают контакт между соседними атомами. Например, ccp представлен никелем, медью и кальцием; hcp выставляется титан, кобальт и магний.
2 закрытых упаковки структуры показаны ниже.Важно отметить разницу между обычными и примитивными элементарными ячейками.
Рисунок 7: Гексагональная плотная упаковка сферы со слоями A и B выделены
Рисунок 8: Обычные и примитивные элементарные ячейки для кубических плотноупакованных сфер; примитивный блок ячейка — ромбоэдр, а обычная элементарная ячейка — куб (отсюда название куб. плотная упаковка).
Ромбоэдрическая решетка Браве имеет периодичность обычная тригональная ячейка, с добавлением два вектора сдвига, $ 2/3 \ mathbf {A} _1 + 1/3 \ mathbf {A} _2 + 1/3 \ mathbf {A} _3 $ и $ 1/3 \ mathbf {A} _1 + 2/3 \ mathbf {A} _2 + 2/3 \ mathbf {A} _3 $. Примитивные векторы можно принять в виде: \ begin {eqnarray} \ label {equ: lat11} \ mathbf {a} _1 & = & ~ \ frac {a} {2} \, \ mathbf {\ hat {x}} — \ frac {a} {\ left (2 \ sqrt {3} \ right)} \ , \ mathbf {\ hat {y}} + \ frac {c} {3} \, \ mathbf {\ hat {z}} \ nonumber \\ \ mathbf {a} _2 & = & \ frac {a} {\ sqrt {3}} \, \ mathbf {\ hat {y}} + \ frac {c} {3} \, \ mathbf {\ hat {z }} \ nonumber \\ \ mathbf {a} _3 & = & — \ frac {a} {2} \, \ mathbf {\ hat {x}} — \ frac {a} {\ left (2 \ sqrt {3} \ right)} \ , \ mathbf {\ hat {y}} + \ frac {c} {3} \, \ mathbf {\ hat {z}}, \ end {eqnarray} а объем примитивной ячейки составляет одну треть от объема обычной ячейки, \ begin {уравнение} V = \ left (\ frac {2} {\ sqrt3} \ right) \, a ^ 2 \, c. 2 \ frac {\ alpha} {2} — 1 \ right)} ~ \ mathbf {\ hat {z}} \ end {массив} \верно).\ end {eqnarray} Дана альтернативная ориентация Сетьявана и Куртароло которые дают только примитивные векторы в этой настройке $ (a ‘, \ alpha) $. Примитивный векторы, используемые для их ромбоэдрической ячейки, различаются из приведенных выше уравнений только ориентацией векторов относительно декартовых осей. Их выбор проще для вычислительных целях, но не показывает взаимосвязь между варианты $ (a, c) $ и $ (a ‘, \ alpha) $.
Мы можем определить ромбоэдрическую решетку двумя способами: как тригональную
решетка с дополнительными векторами трансляции, или как простой
решетка с примитивными векторами одинаковой длины, составляющими равные углы с одним
еще один.Международные таблицы устраняют эту двусмысленность путем
перечисление позиций атомов для ромбоэдрической решетки в шестиугольная установка,
, где все координаты относятся к
обычная ячейка, а в ромбоэдрической настройка,
, где координаты относятся к
ромбоэдрическая решетка. Чтобы еще больше запутать ситуацию,
размеры могут быть представлены в виде $ (a, c) $ или $ (a ‘, \ alpha) $.
В статье можно было бы сказать, что в
ромбоэдрическая ячейка, или 3N атомов в обычной ячейке.Нужно
обратите внимание на контекст.
В базе данных мы сообщим параметры решетки системы
давая $ a $ и $ c $, поскольку это обычная кристаллографическая
практика. Однако мы будем записывать атомные позиции, используя
ромбоэдрические примитивные векторы, поскольку компьютерные вычисления
лучше всего работают с наименьшим числом атомов, необходимых для описания
система.
Пространственные группы, связанные с решеткой ромбоэдра находятся \ begin {array} {lll} 146.~ \ mbox {R3} & 148. ~ \ mbox {R $ \ overline {3} $} & 155. ~ \ mbox {R32} \\ 160. ~ \ mbox {R3m} & 161. ~ \ mbox {R3c} & 166. ~ \ mbox {R $ \ overline {3} $ m} \\ 167. ~ \ mbox {R $ \ overline {3} $ c} & ~ & ~ \\ \ end {массив}
Численное моделирование течения вязкой жидкости над квадратным цилиндром с использованием решеточного метода Больцмана
Эта работа посвящена решеточному расчету Больцмана двумерного несжимаемого вязкого течения через квадратный цилиндр, заключенный в канал.Известно, что природа обтекания цилиндрических препятствий очень сложна. В данной работе расчеты проводятся как для стационарных, так и для нестационарных течений с использованием решеточного метода Больцмана. Подробно изучено влияние числа Рейнольдса, коэффициента закупорки и длины канала. Поскольку были приняты все меры для включения соответствующих показателей в вычислительный метод, эти результаты заслуживают доверия. Подводя итог, настоящее исследование раскрывает многие интересные особенности задачи о квадратном цилиндре и демонстрирует способность решеточного метода Больцмана улавливать эти особенности.
1. Введение
Течение вязкой несжимаемой жидкости вокруг цилиндра квадратного поперечного сечения, ограниченного каналом, также является одной из важных задач вычислительной гидродинамики (CFD) [1–4]. Известно, что наличие стенового ограждения является одним из распространенных примеров во многих практических ситуациях потока (например, дорожные транспортные средства, теплообменники, обтекание высоких зданий, подвесных мостов и т. Д.), А также при исследовании влияния ограждения стен на Решающее значение имеют характеристики поля течения [5–7].Основным преимуществом этой проблемы квадратного цилиндра является относительная простота геометрии по сравнению с круглым цилиндром. Еще одна особенность данной проблемы квадратного цилиндра состоит в том, что она имеет фиксированные точки разделения.
Существующий квадратный цилиндр, заключенный в канал, в основном характеризуется отрывом потока, периодичностью и хорошо известным образованием вихревых дорожек. При очень низком Re поток ламинарный, устойчивый и остается прикрепленным к квадратному цилиндру. По мере увеличения числа Рейнольдса поток отделяется от задней кромки, но остается ламинарным и устойчивым до Re около 50.За пределами этого числа Рейнольдса (Re) возникает неустойчивость, и течение становится периодическим. При этих числах Рейнольдса локализованные области высокой завихренности поочередно сбрасываются с любой стороны цилиндра и конвектируются вниз по потоку. При меньших значениях закритических чисел Рейнольдса течение остается ламинарным. Из-за популярности данной проблемы с точки зрения приложений и важности в литературе доступен ряд экспериментальных и численных результатов для обтекания квадратного цилиндра, установленного в ограниченном канале [8–13].
В большей части доступной литературы расчет поля потока в квадратном цилиндре основан на решении уравнения Навье-Стокса с использованием метода конечных разностей (FDM), метода конечных объемов (FVM) или (или) метода конечных элементов (FEM). В 1984 году Дэвис и др. [1] экспериментально и численно исследовали ограниченное течение через квадратные цилиндры для широкого диапазона Re с различными коэффициентами блокировки, такими как B, = 4 и 6. В 1990 году Franke et al. В [2] представлены численные расчеты ламинарных вихревых течений при обтекании круглых и квадратных цилиндров.В 1992 году Mukhopadhyay et al. [3] провели двумерное численное моделирование обтекания квадратного цилиндра с двумя различными коэффициентами блокировки ( B, = 4,0 и 8,0). В 1993 году Сузуки и др. [4] моделировали обтекание квадратного цилиндра на неэквидистантной сетке для разных диапазонов чисел Рейнольдса и коэффициентов блокировки 5,0 и 20,0. Соханкар и др. В [5, 6] представлены расчеты нестационарного двумерного обтекания квадратного и прямоугольного цилиндров при падении для малых чисел Рейнольдса.В 2000 году Павлов и др. [7] исследовали результаты численных расчетов нестационарного двумерного обтекания квадратного цилиндра несжимаемой жидкости при различных числах Рейнольдса. В 2000 году Breuer et al. [8] также исследовали ограниченный поток вокруг квадратного цилиндра, помещенного внутри плоского канала (коэффициент блокирования B = 8,0), с помощью двух различных численных методов, таких как решеточный автомат Больцмана (LBA) и метод конечных объемов (FVM). В 2002 году Ван и др. В [9] предложен метод дискретных сингулярных сверток-конечных подобластей (DSC – FSM) для анализа вязких течений несжимаемой жидкости для многосвязных сложных геометрий, а именно, обтекания обратного уступа и ламинарного обтекания квадратного цилиндра.В 2004 г. Рой и Бандйопадхай [10] исследовали обтекание квадратного цилиндра, помещенного внутри канала с двумя разными коэффициентами блокировки, а именно 4 и 8 при разных числах Рейнольдса. В 2005 году Абиде и Виаццо [11] представили полезность подхода, основанного на методе проекционной декомпозиции компактной схемы, для двух тестовых задач, а именно, обтекания обращенной назад ступеньки и обтекания квадратного цилиндра. В 2005 году Хасан и др. В [12] также представлен подход для обработки граничного условия истечения, основанный на радиальном поведении поля скорости на больших расстояниях от тела во внешних вязких потоках несжимаемой жидкости.
Развитие решеточного метода Больцмана (LBM) является многообещающим методом, который использует различные нетрадиционные методы для приложений в CFD [14–18]. Сейчас наблюдается, что все большее число исследователей просто используют LBM в качестве альтернативы обычным численным методам для уравнения Навье-Стокса. Чтобы продемонстрировать способность существующего решетчатого метода Больцмана без особого труда обрабатывать потоки по квадратной геометрии, ограниченные в канале, в настоящей работе учитывается влияние расположения стенок канала, то есть эффект блокировки, расположение выходной границы и различные продольные рассматривается расположение цилиндров.Другой целью данной работы является захват нестационарных состояний потока, характеризуемых квадратным цилиндром, при относительно более высоких числах Рейнольдса.
2. Решеточный метод Больцмана
Решеточный метод Больцмана с моделью единственного времени релаксации (LBM-SRT), который является широко используемым LBM, дается [14] следующим образом: где и — функции распределения частиц и равновесия в (), — скорость частицы в направлении th, и — параметр времени единственной релаксации, который контролирует скорость приближения к равновесию.Для моделирования двумерных течений используется двухмерная модель квадратной решетки с девятью скоростями ( D2Q9 ) с девятью дискретными скоростями () (рис. 1).
Дискретный набор скорости записывается как [14] В квадратной решетке D2Q9 предложена подходящая функция равновесного распределения [15]
Добро пожаловать в оптические решетки | Введение в оптические решетки
ВведениеОптическая решетка — это просто набор лазеров на стоячей волне.Электрическое поле этих лазеров может взаимодействовать с атомами — атомы видят потенциал и поэтому собираются в минимумах потенциала. В случае типичной одномерной установки длина волны противоположных лазеров выбирается так, чтобы световой сдвиг был отрицательным. Это означает, что минимумы потенциала возникают в максимумах интенсивности стоячей волны. Кроме того, естественная ширина луча может сделать систему одномерной.
Чтобы атомы не разлетались на слишком большое расстояние, на решетку накладывается дополнительная ловушка.Эта ловушка создается
луч дипольного лазера сфокусирован в месте расположения облака атомов. Перпендикулярно оси луча это создает гауссов профиль интенсивности. Для малых
экскурсии из центра ловушки — это почти гармоническая ловушка. Вдоль
по оси пучка, частота захвата слишком мала: атомы могут разлетаться
из многих 100 м. Чтобы закрыть ловушку в этом направлении, секунда (а позже и
третий) перпендикулярный лазерный луч фокусируется на облако атомов.
Отдых не только для физиков: Wellness Heaven.
Если один из этих лазерных лучей теперь коллимирован после прохождения через облако атомов и отражение в зеркале в обратном направлении, интенсивность и, следовательно, глубина ловушки в центре ловушки удваиваются. Но теперь образуется стоячая волна с его первый узел на поверхности светоотражающего зеркала. Вмешательство Образец тянется обратно к облаку атомов, создавая модуляцию интенсивности с расстоянием в половину длины волны лазера между максимумами интенсивности. Двумерная или трехмерная решетка формируется за счет обратного отражения другого лазера. балки.Стоячие волны пересекаются, и в узлах решетки все стоячие волны имеют максимум интенсивности. Рассмотрим сплюснутые ловушки одного стоячая волна в виде параллельных плоскостей. Тогда две перпендикулярные группы пересекающиеся друг с другом плоскости образуют массив сигарообразных ловушек в регулярной двумерной решетке. Третья группа параллельных плоскостей разделяет 2D узлы решетки в сферически-симметричные ловушки, расположенные в трехмерной оптической решетке.
Нед Батчелдер: Чертежи решеток
Создано 28 июня 2005 г.
Когда я был подростком, я любил рисовать на миллиметровой бумаге.Я придумал много прямолинейных каракулей. Одной из моих специальностей были абстрактные решетки. Например, это простой:
Мне нравится эта решетка, потому что она почти заполняет квадрат, состоит из полностью состоит из петель, симметричен, имеет приятную плотность в центре без будучи просто вылуплением. Недавно я перерисовал его по памяти для своего сына, и это заставило меня задуматься о оригинальные рисунки, которые я сделал с них. Я пошел и нашел некоторых из них.
Изображение выше было создано на компьютере, но 25 лет назад у меня не было этот вариант. Поэтому я остановился на бумаге и карандаше, но не все: Я использовал миллиметровую бумагу и механический карандаш. С помощью этих простых инструментов Я сделал довольно сложные рисунки. Я впадал в состояние, подобное трансу создавая некоторые из них.
Я ценил эту миллиметровку иррационально до такой степени, что постарайтесь не тратить зря. Итак, у меня есть страницы, заполненные рисунками на с обеих сторон (щелкните, чтобы увидеть больше):
Моя техника создания решеток заключалась в том, чтобы начать с вылупленной решетки определенного размера, а затем проделайте в нем дырочки, чтобы изменить форму деталей.Эстетичность упражнения должны были сделать отверстия так, чтобы переплетение было плотным, но не повторяющимся.
Вот одна из решеток с того листа:
Это та же самая решетка, нарисованная компьютером, с (яркой) окраской:
Мне всегда нравилось видеть, как перемещение отверстия может радикально изменить форму то составляющие петли. Конечно, вы не могли бы спроектировать эти вещи, начав с петель. Как их правильно уложить? И работая из дырок «волшебным образом» сделал петли, которые идеально сочетаются друг с другом.
Также на этом листе миллиметровой бумаги был эксперимент с решеткой-решеткой. Это простая решетка показано выше, но каждая прядь заменена на три пряди, которые переплетаются интересным образом, хотя большая часть из них оказалась слишком повторяющейся. Я не знаю, если это это хорошо объясняет:
- Банальность, моя программа для создания этих чертежей.
- Мой блог, где подобные темы появляются время от времени.
Оригинальный рисунок был нарисован механическим карандашом на миллиметровой бумаге толщиной 1 мм. затем сканировали с разрешением 1200 dpi, масштабировали и фильтровали с помощью GIMP.
Рисунки, нарисованные компьютером, были созданы с помощью программы Python. используя aggdraw и Библиотека изображений Python, затем раскрасьте GIMP.
.